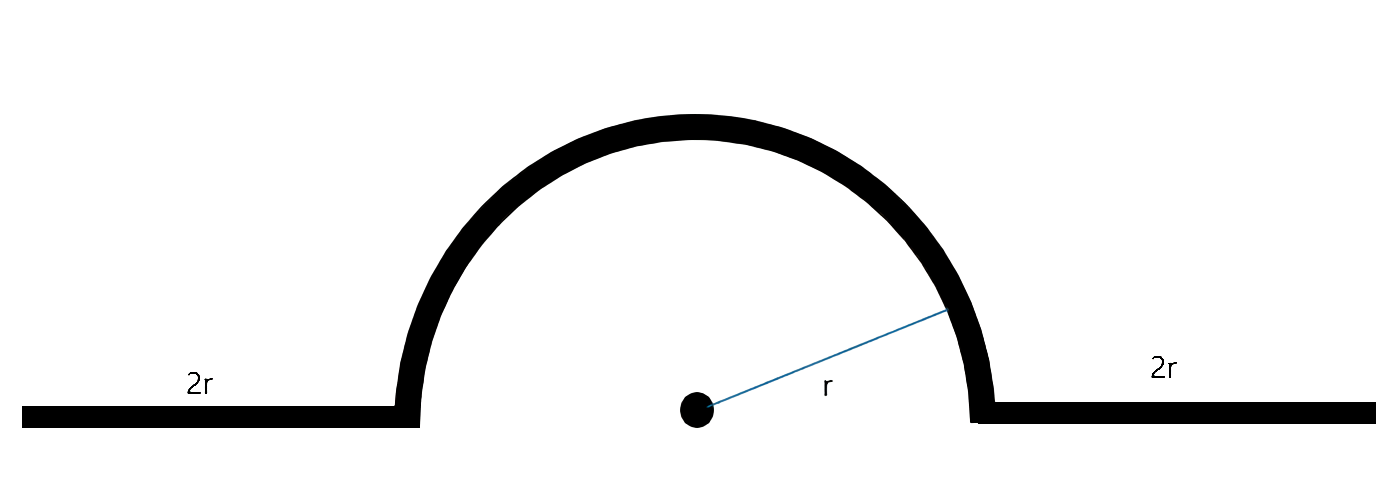
위의 그림처럼 구부러진 도선이 있다.
이 도선은 균일한 전하 밀도 (uniform linear charge density) λ를 갖는다.
그림에 있는 점에서의 전위(electric potential)를 구해보자.
V = ke × q / r , dV = ke × dq / r
이 두가지를 이용하면,
V = ∫ dV = ke × ∫ dq / r
을 유도할 수 있다.
이를 이용하여 계산한다.
위 도선은 양쪽 직선 도선과 구부러진 도선의 세 가지 부분에 의한 전위(electric potential)로 나눌 수 있다.
양쪽 직선 도선에 의한 전위(electric potential)를 각각 V1, V2로, 구부러진 도선에 의한 전위(electric potential)를 V3라고 하자.
그러면 도선에 의한 총 전위 V는
V = V 1 + V 2 + V 3
로 나타낼 수 있다.
(1) V1과 V2, (2) V3 순서로 구해볼 것이다.
(1) V1과 V2
양쪽 직선 도선 위의 한 지점을 정하자. 그러면 직선 도선의 끝에서 그 지점까지의 거리를 l이라고 하자. 그러면 아래와 같이 표현할 수 있다.
직선 도선의 한쪽 끝부터 가운데 점까지의 거리가 3r이므로, 공식에서 r = ( 3r-l )이 되고, q = λl로 나타낼 수 있는 점을 활용해 dq = λdl 로 표현한다.
왼쪽 도선에 의한 전위(electric potential)를 V1으로, 오른쪽 도선에 의한 전위(electric potential)를 V2라고 한다.
V1 = ke × ∫ dq / r = ke × ∫ λdl / ( 3r-l ) = ke λ [ - ln ( 3r - l ) ]
그리고 적분구간은 [0, 2r]이다. 이를 이용해 계산을 하면
ke λ ln3이라는 결과를 얻게 된다.
오른쪽 도선에 의한 전위(electric potential)인 V2는 V1과 크기와 방향이 같으므로
V 1 + V 2 = 2 ke λ ln3 = ke λ ln9
이다.
(2) V3
구부러진 도선 위의 한 지점을 정하자. 그러면 구부러진 도선의 끝에서 그 지점까지의 거리는 rθ이다. 그러면 아래와 같이 표현할 수 있다.
그러면 q = λl = λrθ로 나타낼 수 있으므로, dq = λrdθ로 나타낼 수 있게 된다. 이제 위와 같은 과정을 거쳐 계산해보면 된다.
V3 = ke × ∫ dq / r = ke × ∫ λrdθ / r = keλθ
그리고 적분구간은 [0, π]이다. 이를 이용해 계산을 하면
keλπ
따라서 총 전위 V는
V = V1 + V2 + V3 = ke λ ln9 + ke λ π = ke λ ( ln9 + π )이다.
'일반물리학 > 예제' 카테고리의 다른 글
| Calculating electric field at the point p2 (0) | 2024.11.14 |
|---|---|
| Calculating applied force, and energy rate. (1) | 2024.11.13 |
| Calculating magnetic flux, induced emf, direction of induced current (0) | 2024.11.13 |
| Calculating the induced emf in the coil. (2) | 2024.11.13 |
| 7.00μC인 전하에 가해지는 총 전기력의 크기 (0) | 2024.11.10 |