반응형
- 벡터란?
벡터는 크기와 방향을 모두 가진 물리량을 나타내기 위해 사용되는 개념이다. 벡터는 화살표나 유향선분을 이용해서 나타낸다. 또한 벡터는 굵은 글씨(v)또는 위에 화살표를 붙여 표시한다.
벡터를 화살표를 통해서 나타낼 때, 화살표의 길이는 벡터의 크기를, 화살표의 방향은 벡터의 방향을 나타낸다.
- 벡터의 기하적 표현
예를 들어 어떤 물체가 점 A에서 점 B로 선분을 따라 이동한다고 하면, 해당 운동의 변위벡터 v의 시작점(Initial point)은 점 A이고, 끝점(Terminal point)은 점 B이다.
아래의 그림에서 볼 수 있듯이, 벡터 u는 시작점이 점 C, 끝점이 점 D으로 벡터 v와는 다르지만, v와 평행하며 길이가 같다. 이런 경우에 벡터 u와 벡터 v는 동치(equivalent)벡터, 혹은 같은(equal)벡터라고 한다.

영벡터의 경우에는 0으로 표기하고, 그 길이도 0이다. 영벡터는 특정한 방향을 갖지 않는다.
- 벡터의 합
벡터는 방향과 크기를 모두 갖기에, 단순히 더할 수 없다. 따라서 벡터는 특정 방법을 통해 합을 구하며, 그 방법은 아래와 같다.
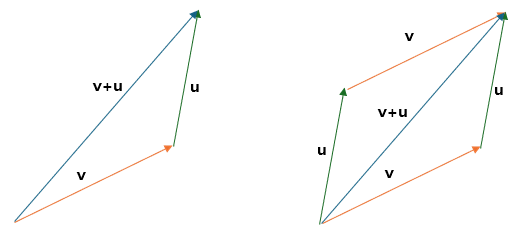
이와 같은 방식을 이용해서 그 합을 구한다.
'미분적분학 > 개념' 카테고리의 다른 글
| - 극좌표에서의 이중적분 (0) | 2024.11.09 |
|---|---|
| - 반복적분과 푸비니 정리 (Fubini's Theorem) (0) | 2024.11.09 |
| - 다중적분 (0) | 2024.11.09 |
| - 거리, 구 (0) | 2024.07.07 |
| - 삼차원 좌표계 (1) | 2024.07.07 |