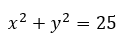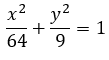f(x,y,z)=x2+y2+z2이고, 영역(domain) W가 중심이 z축( z-axis )이고, 밑면이 z = -1에 있으며, 밑면 반지름 3, 높이가 7인 원기둥이라고 하자. 으로 바꾸어 표현한다고 할 때,A~F, K에 들어갈 값 및 수식과 계산 결과를 구해볼 것이다. 이라는 것을 알아낼 수 있고, 이를 이용해 아래 식을 얻어낼 수 있다. 또한 z의 범위는 아래와 같다. 이를 이용하여 위의 빈칸을 채워보면, 위와 같은 형태를 얻을 수 있다. 이를 계산해보면, 계산 결과는 아래와 같다.