공대생의 공부공간

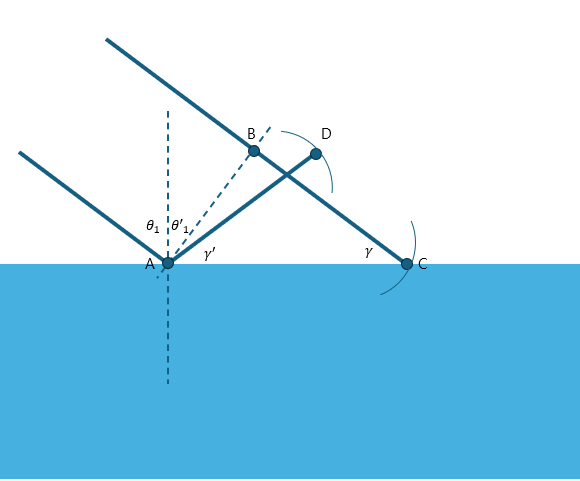
호이겐스의 원리(Huygens' principle)를 이용해서 반사의 법칙을 증명해볼 것이다.(https://thpop.tistory.com/87 / 호이겐스의 원리(Huygens' principle)) 반사의 법칙은 입사각과 반사각이 같다는 법칙이다. 호이겐스의 원리를 이용해 이를 증명해보자. 위와 같이 평행한 두 광선이 입사한다고 가정하자. 아래의 광선 1이 지점  A에서 반사되었을 때, 입사광선이 법선과 이루는 각을 θ1, 반사광선이 법선과 이루는 각을 θ'1이라고 하고, 반사광선이 바닥과 이루는 각을 γ', 광선1과 평행한 광선 2가 바닥과 이루는 각을 γ라고 하자. 또한 지점 B는 A에서 광선 2로 내린 법선이다. 그러면 선분 A는 광선 1이 평면에 반사되는 그 순간의 파면(wave front)..

호이겐스의 원리(Huygens' principle), 혹은 하위헌스 원리라고도 불린다. 호이겐스의 원리 (Huygens' principle) 는 쉽게 말해 이전 파면의 위치로부터 파면의 위치를 결정하여 파동이 어떻게 진행하는지를 알 수 있는 법칙이다. 간단히 표현해서, 위의 그림과 같이 표현할 수 있다. 이전 파면에서부터 일정 시간 동안 진행한 파동들에서 위상이 같은 파동과 공통적으로 접하는 곡선을 찾으면 그것이 새로운 파면이 된다는 것이다. 이는 위의 그림과 같은 직선 파면에서 유효하지만, 직선 파면뿐만 아니라 구형 파면에서도 유효하다. 또한, 호이겐스의 원리(Huygens' principle)를 이용해서 반사의 법칙, 스넬의 법칙의 증명도 가능하다.

이전 내용(https://thpop.tistory.com/84 / 맥스웰 방정식 ··· (1))앞서 알아본 Maxwell's equations를 이용해 전자기파 파동 방정식(electromagnetic wave equation)을 유도할 수 있다. - Faraday's Law 위 Faraday's Law로부터, 아래의 관계식을 유도한다.- Ampere - Maxwell Law 위 Ampere - Maxwell Law로부터, 아래의 관계식을 유도한다.   전자기파 파동 방정식(electromagnetic wave equation)의 유도- wave equation of electric field - wave equation of magnetic field 위와 같은 형태의 wave equation을 얻을 ..

맥스웰 방정식(Maxwell's equations)이란 전자기학에서 전기장과 자기장에 관한 4개의 방정식을 의미한다.전자기학에는 대표적인 4가지 법칙이 있다. - Gauss's Law 어떤 closed surface에서 Electric flux의 총량은 surface 내부의 총 전하량을 ε_0로 나눈 것과 같다는 법칙으로, 위 법칙이 갖는 물리적 의미는 가우스 법칙은 전기장이 전하 분포와 연관되어 있음을 보여준다. - Gauss's Law in magnetism어떤 closed volume을 들어오고 나가는 전기장선(magnetic field lines)의 총량 0이라는 것으로, 위 법칙이 갖는 물리적 의미는 자기 홀극(magnetic monopole)이 존재할 수 없음을 보여준다. - Faraday's..

이중적분, 혹은 삼중적분 같은 다중적분을 수행할 때, dA, dV, dS같은 다양한 종류의 좌표계로 변환을 하는 경우가 생긴다.원하는 차원의 좌표계로 변환할 때 보정해주기 위해서 곱해주는 것이 바로 야코비안 행렬(Jacobian matrix)이다. 야코비안 행렬(Jacobian matrix)의 형태는 아래와 같다. 예시를 통해 살펴보자.앞서 극좌표에서 이중적분의 수행을 알아본 적이 있다.(https://thpop.tistory.com/33 / 극좌표에서의 이중적분) dA => dydx => r drdθ과 같이 변환하는 과정을 거쳤다. 여기서 나오는 r이 바로 야코비안 행렬의 계산 결과이다. 극좌표로 전환할 때, x = r cosθ, y = r sinθ로 변환하는데, 이는 곧 (x,y) → (r, θ)로 ..

문제)(1) F = ▽f가 되는 f를 구하고,(2) (1)의 결과를 이용해 주어진 곡선 C 위에서 선적분 ∫ F·dr을 계산하여라F(x,y) = C : (4,-2) ~ (1,1)까지 쌍곡선 x=y^2위의 호이다.풀이)(1)F(x,y) = 이고, 만약 F = ∇f이면, d(f(x,y))/dx = 2x, d(f(x,y))/dy = 4y이다.그러면 d(f(x,y))/dx = 2x은 f(x,y) = x^2 + K임을,d(f(x,y))/dy = 4y는 f(x,y) = 2y^2 + L임을 나타낸다.이 두가지를 합치면, f(x,y) = x^2 + 2y^2 + A (A는 상수) (2)C는 smooth curve이고, 시작점은 (4,−2), 종점은 (1,1)이므로,  따라서 답은 -21이다.

문제)F(x,y,z) = sy^2z + x^2 , C = {(x,y,z)| x = t^2, y=e^(t^2-1), z=t^2+t, -1 ≤ t ≤ 1},Calculate ∫ ▽f dr풀이)F(x,y,z) = sy^2z + x^2 , C = {(x,y,z)| x = t^2, y=e^(t^2-1), z=t^2+t, -1 ≤ t ≤ 1}이므로,∇f 는 F의 gradient vector field이고, 즉 ∇f 는 conservative하다. 따라서, Line C에서 ∫ ▽f dr = F(1,1,2) − F(1,1,0) = [(1)(1^2)(2) + 1^2] − (0 + 1^2) = 2. 답은 2이다.

f(x,y,z)=x2+y2+z2이고, 영역(domain) W가 중심이 z축( z-axis )이고, 밑면이 z = -1에 있으며, 밑면 반지름 3, 높이가 7인 원기둥이라고 하자. 으로 바꾸어 표현한다고 할 때,A~F, K에 들어갈 값 및 수식과 계산 결과를 구해볼 것이다.  이라는 것을 알아낼 수 있고, 이를 이용해 아래 식을 얻어낼 수 있다.  또한 z의 범위는 아래와 같다.  이를 이용하여 위의 빈칸을 채워보면,  위와 같은 형태를 얻을 수 있다. 이를 계산해보면, 계산 결과는 아래와 같다.

원기둥 좌표계를 사용해 주어진 영역(domain) W에서 f(x,y,z)의 삼중적분을 계산해볼 것이다.※ 참고 : (https://thpop.tistory.com/72 / 삼중적분과 원기둥좌표계(cylindrical coordinate system)) f(x,y,z)와 주어진 영역(domain)은 다음과 같다. f(x,y,z) = z, x^2+y^2 ≤ z ≤ 49 이를 원기둥좌표계로 변환하면,  임을 이용하여, 임을 이끌어낼 수 있고, 그렇게 되면 삼중적분은 다음과 같은 형태가 된다.이를 계산해보면, 답은 아래와 같다.

-  array의 최대 / 최솟값? 주어진 데이터에서 최대, 혹은 최솟값을 흔히 물어본다. 최대, 혹은 최솟값을 얻으려면 모든 모든 요소들을 확인해야 한다. 이를 위해서는 현재의 최댓값, 혹은 최솟값을 저장하는 일시적 변수(temporal variable)을 필요로 한다. 즉 다음 단계들을 거쳐야 한다.1. 변수 선언하기2. 그 변수를 데이터의 upper bound / lower bound로 초기화한다. 예시는 아래와 같다....int min_score = 100; // Upper bound is 100 for scoresfor (int i = 0; i scores[i])min_score = scores[i];... 최솟값을 찾으려면 upper bound를, 최댓값을 찾으려면 lower bound를 정..