공대생의 공부공간

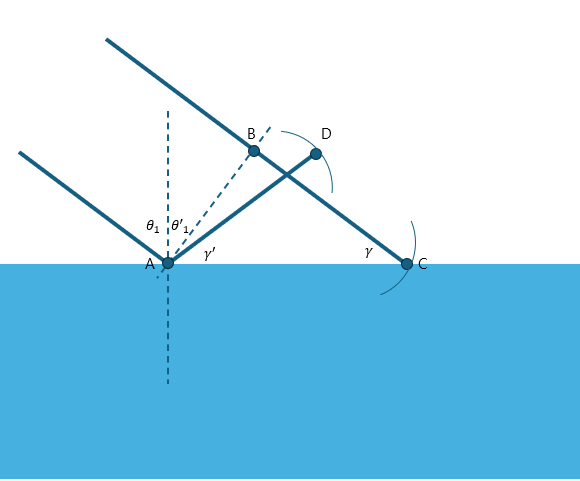
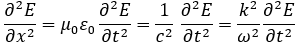이전 내용(https://thpop.tistory.com/94 / 맥스웰 방정식 ··· (3)) 앞서 전자기파 파동 방정식(electromagnetic wave equation)의 해에 대해 알아봤었고, 이번에는 그 해가 맞는지 검증해볼 것이다. 검증에 앞서 두 가지를 확인할 것이다.(1)wave equation과 electromagnetic wave equation을 이용하여 아래 식을 유도하면, 전자기파의 속력 c는 아래와 같이 표현된다.(2)식을 좌변으로 이항하면 아래와 같은 관계식을 얻을 수 있다.  전자기파 파동 방정식(electromagnetic wave equation)의 해는 다음과 같다. 이를 전자기파 파동 방정식(electromagnetic wave equation)에 넣어보자. 따라서..

이전 내용(https://thpop.tistory.com/85 / 맥스웰 방정식 ··· (2))  앞서 전자기파 파동 방정식(electromagnetic wave equation)을 유도했었고, 이번에는 그 해에 대해 알아볼 것이다. 아래 식이 wave equation이다.여기서 v는 wave의 속력이다.그리고  electromagnetic wave의 속도는 빛의 속도인 c이다. (c = 2.9979 × 10^8 m/s)  전자기파 파동 방정식(electromagnetic wave equation)의 해는 아래와 같이 표현된다.여기서 k는 wave number이고, ω는 각진동수(angular frequency)로, 이 두가지는 아래와 같은 방식으로 구할 수 있다.이 두 가지 wave number인 k와..

앞서 Toroid에서의 self inductance를 구해보았다.(https://thpop.tistory.com/92 / Toroid에서의 self-inductance) 문제)마찬가지의 조건에서(b) Toroid에 저장된 total magnetic energy를 구하라. 풀이)(b)Toroid의 total energy stored in the magnetic field는 전체 부피를 통해 적분함으로써 구할 수 있다.우선 자기장의 energy density를 구하고, 이를 부피에 대해서 적분한다. energy density는 다음과 같다. dV = (2πrh)dr으로 변환 가능함을 이용해 계산해보면 에너지는 다음과 같다. 또한 toroid의 경우, 구한 stored energy와 아래 공식을 이용하여 se..

문제)솔레노이드를 도넛처럼 원형 형태로 말은 형태가 바로 Toroid이다.이번 예제에서는 Toroid가 rectangular cross section을 갖는다고 가정한다. 코일의 감긴 횟수를 N, 안쪽까지의 반지름을 a, 바깥쪽까지의 반지름을 b, rectangular cross section의 높이를 h라고 하자. (a) self-inductance를 구하시오.  풀이)(a)toroid의 대칭성으로 고려하면, toroid 내부의 자기장은 원형임을 알 수 있다.따라서 Ampere's Law를 적용함에 있어서, 적분 경로를 원의 반지름 r로 정해야 한다. 그러므로 아래와 같다. Toroid의 코일의 한 회전을 통과하는 magnetic flux는 rectangular cross section에서 적분함으로써..

문제)아래 그림과 같은 솔레노이드가 있다고 가정하자.길이는 l, 감긴 횟수는 N, 반지름은 R이라고 가정한다. (a) self-inductance를 구하시오(b) 전류 I가 코일을 지났을 때, stored energy를 구하시오. 풀이)(a)Ampere's Law에 의해, 솔레노이드 내부의 자기장은 아래와 같다.n은 단위 길이 당 감긴 횟수이다.  각 회전 당 magnetic flux는 아래와 같이 표현할 수 있다. 그러므로, self-inductance는 아래와 같다. (b)저장된 에너지는 공식에 따라 아래와 같다.또한 위의 공식에서 알 수 있는 것은, πR^2 l은 솔레노이드의 부피이므로, B^2 / (2μ0)는 에너지 밀도임을 알 수 있다.

Thomas Young의 이중 슬릿 실험을 통해, light wave 사이에는 간섭(interference)가 일어난다는 것이 밝혀졌다. - 상쇄 간섭 (destrictive interference) 상쇄 간섭(destructive interference)은 위상이 반대인 두 파동이 중첩될 때의 간섭이며. 마루와 골이 만나서 합성파의 진폭이 작아진다. 만약 상쇄 간섭으로 진폭이 0이 되면 소멸된다.  - 보강 간섭 (constructive interference) 보강 간섭 (constructive interference)은 같은 위상의 두 파동이 중첩될 때 일어나는 간섭이며, 마루와 마루 또는 골과 골이 만나 파동의 진폭이 더 커진다.

호이겐스의 원리(Huygens' principle)를 이용해서 스넬의 법칙을 증명해 볼 것이다.(https://thpop.tistory.com/87 / 호이겐스의 원리(Huygens' principle)) 스넬의 법칙은 빛이 굴절률 n1​인 매질에 입사각 θ1​으로 입사하면, 빛은 두 매질의 경계면에서 반사되는 빛과 굴절률 n2​인 매질에 투과되어 굴절되는 빛이 생기며 굴절되는 빛이 법선과 이루는 각을 θ2라고 하면 아래와 같은 관계가 성립한다는 법칙이다. n1 sin θ1 = n2 sin θ2 호이겐스의 원리를 이용해 이를 증명해보자.  위와 같이 평행한 두 광선이 입사한다고 가정하자. 입사한 광선이 범선과 이루는 각을 θ1, 입사한 광선이 굴절된 후, 굴절된 광선이 법선과 이루는 각을 θ2라고 하자...

호이겐스의 원리(Huygens' principle)를 이용해서 반사의 법칙을 증명해볼 것이다.(https://thpop.tistory.com/87 / 호이겐스의 원리(Huygens' principle)) 반사의 법칙은 입사각과 반사각이 같다는 법칙이다. 호이겐스의 원리를 이용해 이를 증명해보자. 위와 같이 평행한 두 광선이 입사한다고 가정하자. 아래의 광선 1이 지점  A에서 반사되었을 때, 입사광선이 법선과 이루는 각을 θ1, 반사광선이 법선과 이루는 각을 θ'1이라고 하고, 반사광선이 바닥과 이루는 각을 γ', 광선1과 평행한 광선 2가 바닥과 이루는 각을 γ라고 하자. 또한 지점 B는 A에서 광선 2로 내린 법선이다. 그러면 선분 A는 광선 1이 평면에 반사되는 그 순간의 파면(wave front)..

호이겐스의 원리(Huygens' principle), 혹은 하위헌스 원리라고도 불린다. 호이겐스의 원리 (Huygens' principle) 는 쉽게 말해 이전 파면의 위치로부터 파면의 위치를 결정하여 파동이 어떻게 진행하는지를 알 수 있는 법칙이다. 간단히 표현해서, 위의 그림과 같이 표현할 수 있다. 이전 파면에서부터 일정 시간 동안 진행한 파동들에서 위상이 같은 파동과 공통적으로 접하는 곡선을 찾으면 그것이 새로운 파면이 된다는 것이다. 이는 위의 그림과 같은 직선 파면에서 유효하지만, 직선 파면뿐만 아니라 구형 파면에서도 유효하다. 또한, 호이겐스의 원리(Huygens' principle)를 이용해서 반사의 법칙, 스넬의 법칙의 증명도 가능하다.

이전 내용(https://thpop.tistory.com/84 / 맥스웰 방정식 ··· (1))앞서 알아본 Maxwell's equations를 이용해 전자기파 파동 방정식(electromagnetic wave equation)을 유도할 수 있다. - Faraday's Law 위 Faraday's Law로부터, 아래의 관계식을 유도한다.- Ampere - Maxwell Law 위 Ampere - Maxwell Law로부터, 아래의 관계식을 유도한다.   전자기파 파동 방정식(electromagnetic wave equation)의 유도- wave equation of electric field - wave equation of magnetic field 위와 같은 형태의 wave equation을 얻을 ..